Dean's blog
0%

R-卡方检验

Posted on
Symbols count in article: 2.8k Reading time ≈ 3 mins.

chi-squared test

χ2检验主要有三个用途：单样本方差的同质性检验、独立性检验和适合性检验。适合性检验和独立性检验都是应用于离散型资料的假设检验，其基本原理是通过χ2值的大小来检验观测值（observed value, O）**与理论值（expected value, E）**之间的偏离程度。

在本文中，我们先介绍独立性检验和适合性检验在R语言当中的应用。

在R中，卡方检验的函数是chisq.test()

chisq.test() :
chisq.test performs chi-squared contingency table tests and goodness-of-fit tests

1
2
3
chisq.test(x, y = NULL, correct = TRUE,
           p = rep(1/length(x), length(x)), rescale.p = FALSE,
           simulate.p.value = FALSE, B = 2000)

x : 进行检验的数据，可以是vector或matrix

y : 进行检验的数据，当x是matrix时，y会被忽略，x和y可同时为factor。

correct : 该逻辑参数控制2x2列联表的独立性检验时，是否进行连续性矫正，即对所以|O-E| - 0.5

p : 为输入的概率值，应与x变量的长度一致。注意p不可以为负数

rescale.p : 该逻辑参数控制是否将p的和重新调整为1

simulate.p.value : 控制是否以蒙特卡洛采样的方法模拟p值

B : 为蒙特卡洛采样的重复次数。

使用chisq.test要更加注意在卡方检验中：

  • 零假设H0就是观测值与理论值无显著差别。

  • 备择假设HA是观测值与理论值有显著差别。

具体到适合性检验的话，H0：观测值符合某个理论分布；HA：观测值不符合某个理论分布。

对于独立性检验而言，H0：事件A与事件B无显著关系，即A与B相互独立；HA：事件A与事件B相关。

适合性检验

适合性检验（compatibility test）是比较观测值与理论值是否符合的假设检验。在生物学研究中，有很多情况都会使用到适合性检验，也成为拟合优度检验，下面我们以孟德尔经典的例子来展示chisq.test() 在适合性检验方面的应用。

【例1】 孟德尔用豌豆的两对相对性状进行杂交实验，黄色圆滑种子与绿色皱缩种子的豌豆杂交后，F2代分离的情况为：黄圆315、黄皱101、绿圆108、绿皱32，共556粒，问此结果是否符合自由组合定律9:3:3:1？

1
2
3
4
5
6
7
8
> x <- c(315, 101, 108, 32)  #输入样本资料
> p <- c(9/16, 3/16, 3/16, 1/16)  #输入待检验的比例
> chisq.test(x, p = p)

	Chi-squared test for given probabilities

data:  x
X-squared = 0.47002, df = 3, p-value = 0.9254

chisq.test直接的输出值包括了：卡方值、自由度和p值。

从以上的p值来看，这次检验也是接受H0，即实验结果符合自由组合定律的。

独立性检验

独立性检验（independent test）是判断两个或两个以上因素之间是否具有关联关系的假设检验，常用列联表进行检验。而列联表又可分为2 x 2，2 x c ， r x c的形式（r ≥ 3， c ≥ 3），然而实则上三种列联表的计算大同小异，不同的只是2 x 2列联表需要进行连续性矫正。下面将分别以几个例子展示chisq.test() 在独立性检验方面的应用。

2 x 2列联表

【例2】 现随机抽样对吸烟人群和不吸烟人群是否患有气管炎进行调查，试检验吸烟与患气管炎有无关联？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
> tab <- as.table(cbind(c(50,5), c(250,195)))  #创建列联表
> dimnames(tab) <- list(c("smoker", "non-smoker"),
+                       c("illness", "un-illness"))
> tab
           illness un-illness
smoker          50        250
non-smoker       5        195
> tab_Xsqtest <- chisq.test(tab)
> tab_Xsqtest

	Pearson's Chi-squared test with Yates' continuity correction

data:  tab
X-squared = 23.174, df = 1, p-value = 1.48e-06

在本例中：

H0：吸烟与患气管炎无关。

HA：吸烟与患气管炎有关。

另外，由于是2 x 2列联表独立性检验，自由度小于2，因此进行了连续性矫正。检验的p值小于0.01，说明吸烟与患气管炎有关联。同时，我们还可以注意到chisq.test还会输出其他的内容（但并没有直接打印出来）

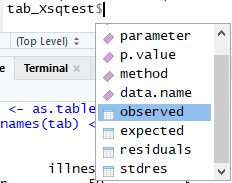
包括了：

  • 样本的观测值
  • 样本的理论值
  • 计算的残差和标准化后的残差

当我们需要使用这些数据时，不妨将检验的结果保存在一变量中，以便调用。

2 x c列联表

【例3】 现随机抽样对性别和参与的党派进行调查，检验性别与党派是否有关。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
> M <- as.table(rbind(c(762, 327, 468), c(484, 239, 477)))
> dimnames(M) <- list(gender = c("F", "M"),
+                     party = c("Democrat","Independent", "Republican"))
> M
      party
gender Democrat Independent Republican
     F      762         327        468
     M      484         239        477
> Xsq <- chisq.test(M)
> Xsq

	Pearson's Chi-squared test

data:  M
X-squared = 30.07, df = 2, p-value = 2.954e-07

卡方检验的p值小于0.01，说明性别与党派是有显著关系的。

可以注意到，2 x c 列联表和2 x 2的代码，除了输入数据的差别外，其他也是几乎一致的。而r x c的代码也是更换输入数据的差别而已。

最后，独立性分析反过来想的话，其实就是相关性分析，因此卡方检验也可以在相关性分析中有用武之地。

当然，Pearson Correlation和Fisher’s exact test也是更为常用的相关性分析，有机会的话也会在后续的文章中向大家介绍这些方法。

卡方检验的R语言实例就介绍到这了，如有不足，请各位指出。

Ref:

《生物统计学》（第五版）李春喜等著

完。