Neighbor Joining是一种bottom-up的聚类方法，常被用于**系统发育树(phylogenetic tree)*的构建当中。 Naruya Saitou 和 Masatoshi Nei在1987年将NJ法发表在Molecular Biology and Evolution*中，至今已有超5万的引入量，实在是生物信息学中超重量级的文章。

P.S. 由于本人对图论一知半解，所以后面写的时候可能各种术语穿插使用，望见谅。

术语阐明

taxa = node = 节点
edge = 边

算法原理

NJ法要求输入的数据必须是**待聚类数据(taxa)**之间的距离信息，例如对多个物种进行NJ法建树的话，输入的就是物种之间的进化距离。

NJ法是一种bottom-up的聚类，故首先要计算出进化距离最近的两个物种，将其聚为一类，再计算出距离该新类最近的一个物种再次聚为一个类，如此迭代，遍历所有输入的物种，构建系统发育树。

下面以对多个物种进行NJ法建树来简述其原理：

Q-criterion

对于n ＞ 3的物种集合X而言，基于现有的距离矩阵 d(x, y)可以计算得到Q矩阵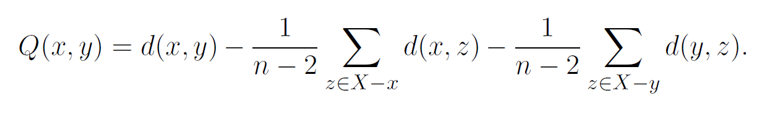

可将**Q(x,y)**视为计算一种矫正后的d(x,y)

选定x,y使得上述Q值最小，即为当前最靠近的两个taxa，而该法即为Q-criterion

构建新节点

找出了距离最近的（x,y）后，构建一个新的节点 Vx,y 取缔原有的两个节点（x,y），接下来可计算x,y点到新节点的距离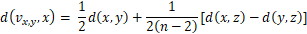

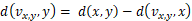
以及$V_{x,y}$ 到其余各点的距离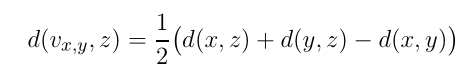

z: 在集合X中除x，y之外的各点

重新进行Q-criterion

上述两步结束后，就对集合X中最近的两点聚类完毕，继续迭代即可对集合中所有的点进行聚类，并构建发育树。

R应用的例子

这里用4个物种同源基因的进化距离矩阵进行NJ法建树，当然更一般来说我们会利用多重序列比对（Multiple Sequence Alignment，MSA），再根据MSA的结果得到进化距离矩阵构建系统发育树

现有4个物种的同源基因ABCD，它们的进化距离矩阵如下：
| | A | B | C | D |
| —- | —- | —- | —- | —- |
| A | 0 | | | |
| B | 5 | 0 | | |
| C | 12 | 11 | 0 | |
| D | 10 | 9 | 8 | 0 |

现将距离矩阵导入R中，使用R包ape的nj()函数建树

library(ape)

A <- c(0,5,12,10)
B <- c(5,0,11,9)
C <- c(12,11,0,8)
D <- c(10,9,8,0)
em <- as.matrix(cbind(A,B,C,D))
row.names(em) <- c('A','B','C','D')
tr <- nj(em)
plot(tr)

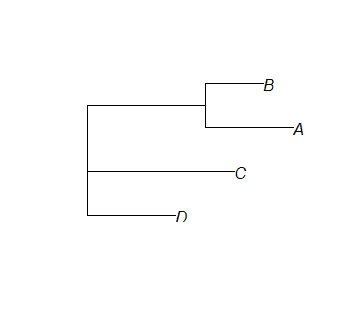
使用参数type可以控制输出有根树或无根树

1	plot(tr, type = "unrooted", rotate.tree = 90)

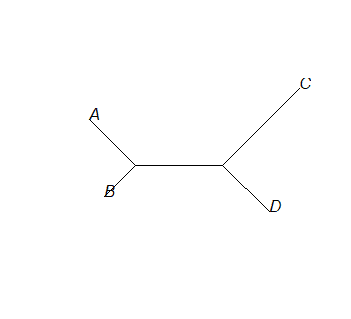
节点的距离，边的长度等信息，亦包含在nj()输出的结果中

str(tr)
## List of 4
## $ edge       : int [1:5, 1:2] 5 5 5 6 6 4 3 6 1 2
## $ edge.length: num [1:5] 3 5 4 3 2
## $ tip.label  : chr [1:4] "A" "B" "C" "D"
## $ Nnode      : int 2
## - attr(*, "class")= chr "phylo"
## - attr(*, "order")= chr "cladewise"

利用R包ggtree可以将edge length 标在树上

library(ggtree)
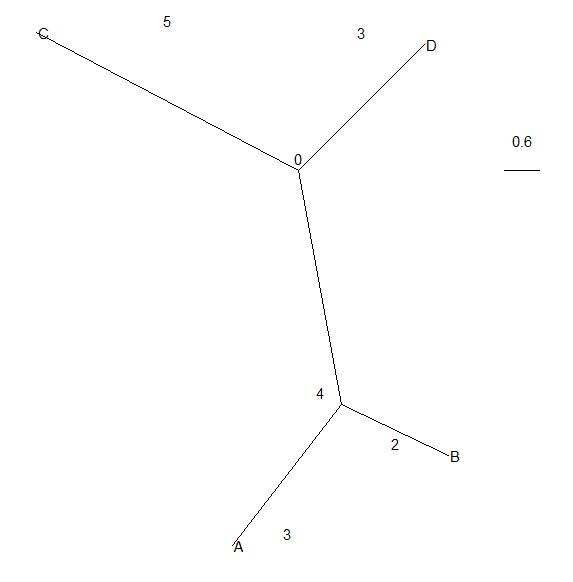
ggtree(tr, layout = 'unrooted') + 
  geom_treescale() +
  geom_tiplab() + 
  geom_text(aes(label=branch.length, x=branch), vjust=-.5)

一点补充：
对同源基因/蛋白进行建树时，物种间的进化距离矩阵一般通过核酸/蛋白质序列的多序列比对（Multiple Sequence Algnment, MSA）结果而来。但如何从MSA的序列比对得分矩阵得到进化距离矩阵暂时还不清楚，以后有待补充。

Ref: en.wikipedia.org/wiki/Neighbor_joining

完。

Dean's blog

理论-Neighbor Joining建树浅析