R-sampling

本文简单介绍几种重抽样方法 (in R)。

Permutation
Bootstrap
Jackknife
Cross validation

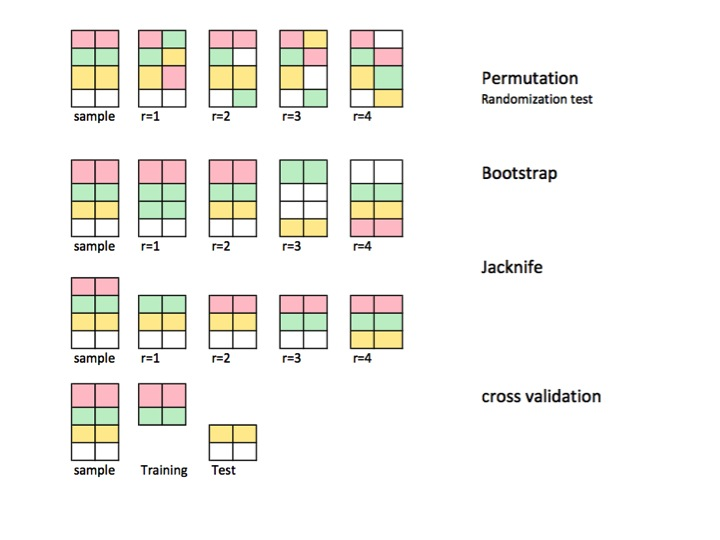
我们生成一组数据，其中x是我们的观测值，y是我们对其的标签。

# generate random data
set.seed(1111)
x <- c(rnorm(10), rnorm(10, mean=5, sd=5))
y <- c(rep("A", 10), rep("B", 10))
df1 <- data.frame(x,y)
str(df1)

1
2
3

## 'data.frame':    20 obs. of  2 variables:
##  $ x: num  -0.0866 1.3225 0.6397 1.1748 0.1163 ...
##  $ y: chr  "A" "A" "A" "A" ...

Permutation

Permutation相当于是一种无放回的重抽样方法，通常用于假设检验。

1
2
3

# single permutation 
set.seed(2222)
sample(df1$x, replace = FALSE)

##  [1]  9.31952342 -0.08658011  5.56155482  3.71174074  1.17478657  0.63970204
##  [7] -2.93084636  0.18759838  1.38404752  1.28394086  0.11629031  6.77816542
## [13]  1.11777194  0.11760093 -4.08500801  1.32252443  4.59743697 -2.67140783
## [19]  0.67750806  9.95418174

我们可以使用Permutation test检验A，B两组的值是否有差异

# permutation test (n=1000)
set.seed(3333)
permt.ls <- list()
for (i in 1:1000) {
  permt.i <- sample(df1$x, replace = FALSE)
  # calculate the mean of difference from permutated samples
  diff.i <- abs(mean(permt.i[1:10]) - mean(permt.i[11:20]))
  permt.ls[[i]] <- c(permt.i, diff.i)
}
permt.df <- Reduce(rbind, permt.ls)
diff.raw <- abs(mean(df1$x[1:10]) - mean(df1$x[11:20]))
# Calculate the p-value
mean(permt.df[,21] >= diff.raw)

1	## [1] 0.079

每一次重抽样后，我们都可以计算两组样本均值的差异。如果重抽样样本组间差异大于原始样本组间差异的话，可以认为是一次错误事件，通过计算错误事件在总重抽样次数中的占比就可以得到置换检验的p值。

在这里1000次重抽样中，只有79次是错误事件，所以我们的p值为0.079

Bootstrap

Bootstrap是一种有放回的重抽样方法，通常用于参数估计。

1
2
3

# single bootstrap
set.seed(4444)
sample(df1$x, replace = TRUE)

##  [1]  1.1177719  9.9541817 -2.9308464  0.1875984 -2.9308464 -4.0850080
##  [7] -4.0850080  4.5974370  0.1162903  0.6397020  6.7781654  4.5974370
## [13]  1.3225244  9.3195234  1.2839409 -4.0850080  0.6397020  1.1177719
## [19]  0.6775081  3.7117407

例如，我们用bootstrap估计总体的均值

set.seed(5555)
mean.raw <- mean(df1$x)
mean.i <- c()
# bootstrap (n=1000)
for (i in 1:1000) {
  boot.i <- sample(df1$x, replace = TRUE)
  mean.i[i] <- mean(boot.i)
}
mean.boost <- mean(mean.i)
mean.raw; mean.boost

1
2
3

## [1] 1.908527

## [1] 1.956184

此外，我们还可以计算bootstrap预测均值的标准误（SE）

1
2
3

# calculate the standard error 
mean.se.boost <- sqrt(sum((mean.i - mean.boost)^2)/(1000-1))
mean.se.boost

1	## [1] 0.788522

Jackknife

Jakknife可以被认为是一种leave-one-out的重抽样方法，对于大小为k的数据集，将产生k个大小为k-1的样本.

jack.ls <- list()

for (i in 1:nrow(df1)) {
  jack.ls[[i]] <- df1[-i,]
}

length(jack.ls); dim(jack.ls[[1]])

1
2
3

## [1] 20

## [1] 19  2

Cross validation

交叉验证将数据切分为测试集和验证集，常在模型拟合中使用。例如k-fold cross validation将数据划分为k组不重叠的数据集。

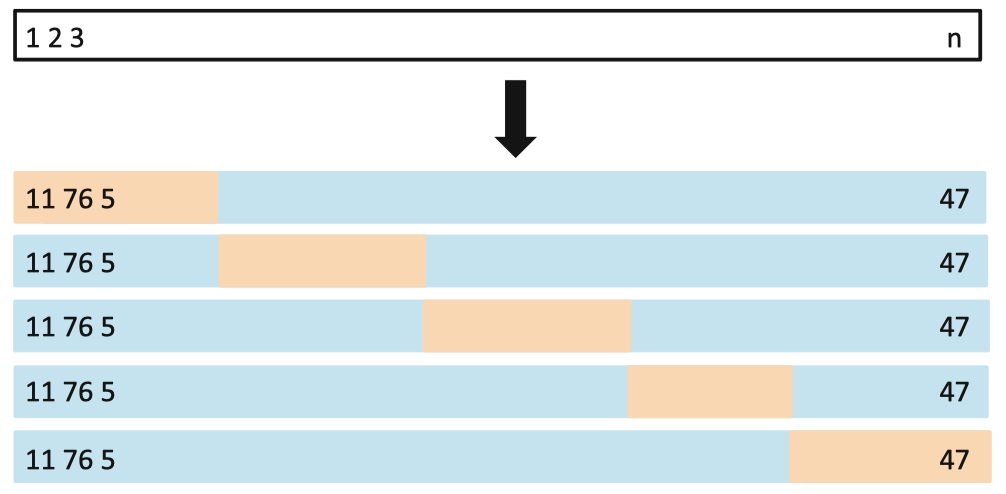
Figure: Illustration of 5-fold CV (https://yey.world/2020/08/31/MAST90083-05/).

# 1-fold cv
set.seed(6666)
training_size <- round(nrow(df1)*0.7)
training_idx <- sample(nrow(df1), size = training_size, replace = FALSE)
training_set <- df1[training_idx,]
val_set <- df1[-training_idx,]

nrow(training_set); nrow(val_set)

1
2
3

## [1] 14

## [1] 6

有时候，由于样本量太小，无法满足k-fold CV中不重叠分组的要求，有的样本不可避免地被重复使用。

# 5-fold cv
set.seed(7777)
fold_idx <- list()
val_size <- nrow(df1) - training_size
all_idx <- 1:nrow(df1)
for (i in 1:5) {
  fold_idx_i <- unique(unlist(fold_idx))
  if (all(all_idx %in% fold_idx_i) | is.null(fold_idx_i)) {
    fold_idx[[i]] <- sample(all_idx, val_size, replace = FALSE)
  } else if (val_size < length(all_idx[-fold_idx_i])) {
    fold_idx[[i]] <- sample(all_idx[-fold_idx_i], val_size, replace = FALSE)
  } else if (val_size > length(all_idx[-fold_idx_i])) {
    fold_idx[[i]] <- c(all_idx[-fold_idx_i], sample(all_idx, val_size-length(all_idx[-fold_idx_i]), replace = FALSE))
  }
}
fold_data <- lapply(fold_idx, function(i) {
  list(training = df1[-i,], valdation = df1[i,])
})
fold_idx

## [[1]]
## [1] 16  3 19  5 15 14
## 
## [[2]]
## [1] 13  1 18  4  9 17
## 
## [[3]]
## [1]  7 20  6  8  2 12
## 
## [[4]]
## [1] 10 11 14 13  7 15
## 
## [[5]]
## [1]  3 10  2  5 15 12

以上就是对重抽样方法的简单介绍。

Ref:

https://stats.stackexchange.com/questions/104040/resampling-simulation-methods-monte-carlo-bootstrapping-jackknifing-cross

https://yey.world/2020/08/31/MAST90083-05/